Doctoral Research

Microscale fluid-structure interactions (FSIs) have aroused the attention of the scientific community because internal flows in compliant micro-conduits are often encountered in microfluidics. Although previous studies investigated the microscale FSIs from various perspectives, a unified understanding of the physics is lacking. My doctoral research aims to put forward a general theoretical framework for Newtonian fluids flowing through compliant micro-conduits. I have constructed a reduced one-dimensional (1D) model, with which, I have analyzed the steady responses, the nonlinear dyanmics and the stabilities of such microsystems, providing new insights into the physics of FSIs at the microscale.

1. Inertialess flow in compliant microchannel: nonlinear flow rate-pressure drop relation

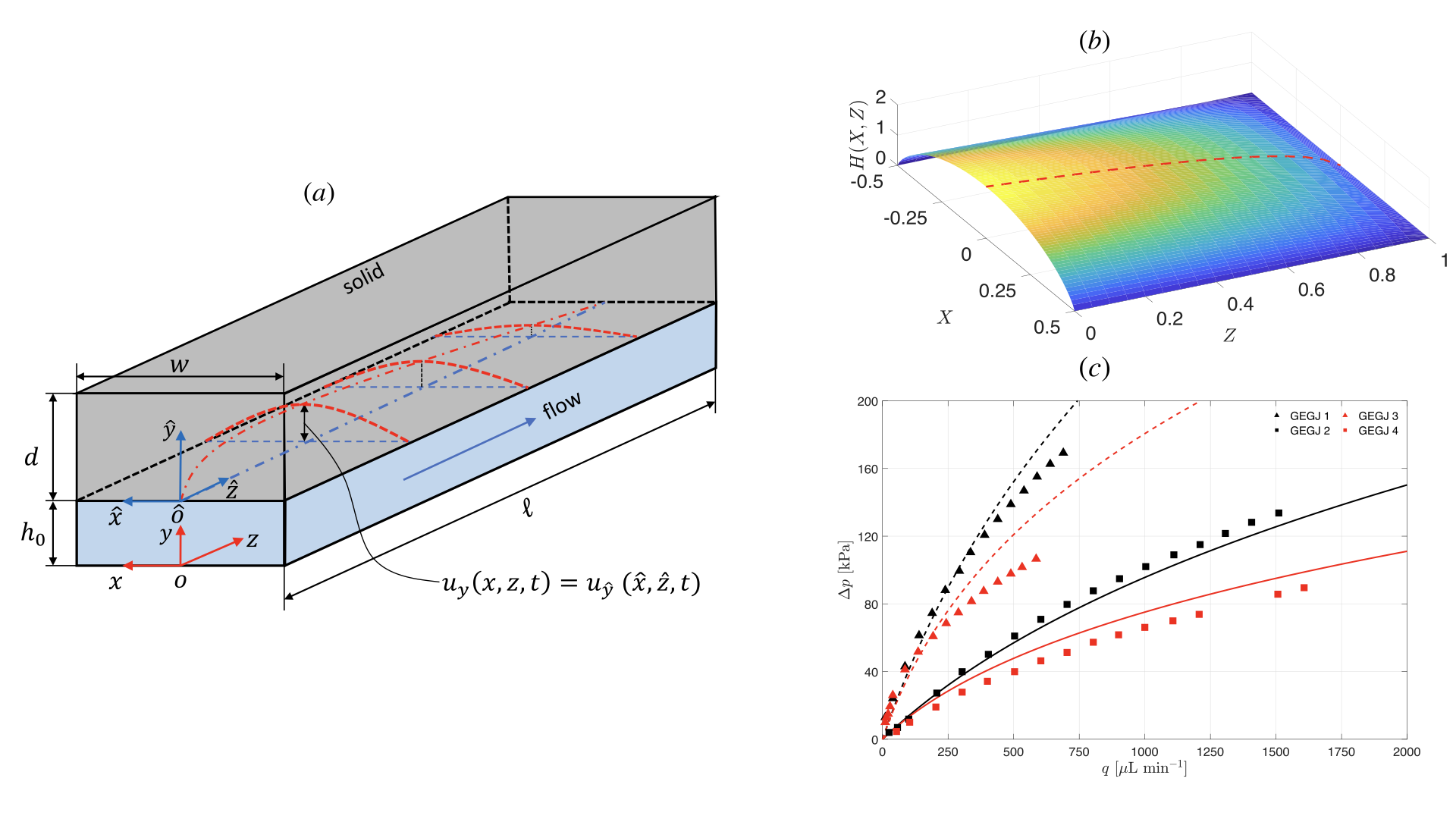Figure 1. (a) A typical configuration of a Newtonian fluid flowing through a rectangular microchannel with a deformable top wall. (b) The predicted deformed fluid-solid interface at the leading order. (c) The nonliear flow rate-pressure drop relation at steady state. The curves are from the predictive theory, while the dots are experimental data published by Gervais et al (2006).

For a Newtonian fluid, due to FSI, the pressure drop required to maintain a steady flow varies nonlinearly with the flow rate, significantly deviating from the classic Poiseuille’s or Hagen-Poiseuille’s law in rigid conduits. Quantifying this nonlinear flow rate-pressure drop relation is important in the design of microfluidic devices. Based on the perturbation method, we have analyzed the FSI of a Newtonian fluid flowing through a commonly used thick-walled microchannel (Figure 1a) in the regime of inertialess flow. We have successfully derived a first fitting-parameter-free theory to predict the nonlinear flow rate-pressure drop relation, which rationalizes the experimental measurements performed at MIT in 2006 (Figure 1c).

2. Generalization: microscale FSI with finite fluid inertia

As many microfluidic devices are operated under higher flow rates, finite fluid inertia needs to be taken into account when investigating the microscale FSIs. We would like to develop a generalized theory which accounts for finite fluid inertia and applies to microchannel systems with different geometrical properties. Noting that most of microchannels are made slender, we first extend the classic lubrication approximation for the flows by incluidng finite fluid inertia through a scaling analysis. Then, we show that, with linear elasticity, across a large range of wall thickness, the wall slenderness gives rise to a Winkler-foundation-like behavior of wall deformation. The two findings motivate us to build a reduced system shown in Figure 2a.

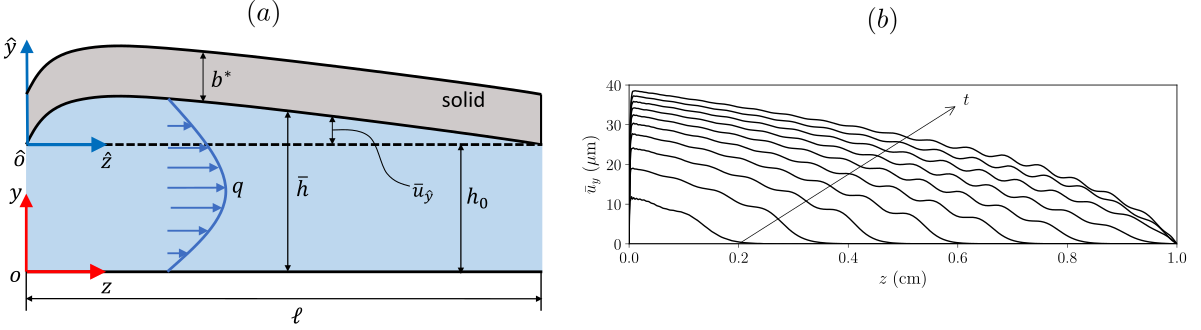Figure 2. (a) The deformed steady state of the reduced FSI system. (b) An example of the time evolution of the fluid-solid interface shape from the undeformed intial state. In this case, the system is found to be linearly unstable.

3. Towards dynamics: FSI-induced global instabilities

Even though the Reynolds number of microscale flows are typically low (up to several hundreds), far below the well-documented critical value of hydrodynamic instabilities, surprisingly, previous experiments reported that FSI could trigger instabilities in soft microchannel flows at this low Reynolds nummber. This observation indicates that FSIs could be exploited to enhance microscale mixing. To understand the FSI-induced instabilities, we construct a new 1D FSI model by consistently reducing the system from 3D to 1D, without introducing any fitting parameters. The steady and unsteady behaviors of the model agree qualitatively well with previous experimental observations, capturing key effects. Importantly, global unstable modes are predicted in the 1D system. The time evolution of the fluid-solid interface in the globally unstable case is shown in figure 2b. Also see an example video below.

The video shows the nonlinear dynamics of a globally unstable microchannel system. The fluid-solid interface evoloves in time with transverse waves proporgating back and forth. Self-sustained oscillations are triggered and self-sustained due to FSI.

Ongoing research

1. The nonlinear dynamics of the new 1D FSI model

The dynamic behaviors of the new 1D FSI model in the parametric plane are yet determined. I have developed computational tools (strongly-implicit finite-difference schemes and pseudospectral methods) to accurately integrate the governing equations, including capturing the fast-time-scale oscillatory behaviors. Interestingly, from these simulations, I observe that if multiple unstable modes co-exist, the 1D reduced system is sensitive to initial conditions and displays a chaos-like behavior. Currently, we are building a reduced model through Galerkin truncation to unravel the effect of mode interactions and nonlinearities in the system.

2. The FSIs in a compliant tube with prescribed oscillatory pressure drop

Fluids conveyed in a tube with a prescribed pressure drop are commonly seen in biological flows. What if the tube is made from soft materials? Currently, I am participating in a collaborative project trying to understand the FSIs in an oscillatory tube flows. We have constructed a 1D reduced model by coupling the Womersley velocity profile with linear elasticity, and observed FSI-induced streaming in the system. To validate our reduced model, we are also conducting direct numerical simulations via SvFSI of SimVascular.

Past research

1. Steady-state scalings and the linear stability of a one-dimensional system with lubrication flows coupled with nonlinear Euler-Bernoulli Beam (paper).
2. Master’s thesis: Predicting ship motions in waves using the indirect time-domain method
   • Derived a new Kramers-Kronig relations for ships with forward constant speed
   • Wrote a solver with FORTRAN to predict ship motions in time domain by transforming the hydrodynamic coefficients from the frequency-domian simulations based on the boundary element method
   • Studied the parametric roll of ships by calculating the restoring forces on the instantaneous wet surfaces